Using expected value when donating to charity — and day-to-day

If only we never had to make any choices. How easy, stress-free, and wonderfully dull life would be. What’s for dinner? Whatever’s closest at hand. Where to invest my savings? Leave the money wherever it is and hope for the best.

But part of the condition of being a human adult is the need to make countless decisions, large and small, hoping always to choose the option with the most satisfying or beneficial outcome — or on occasion, the one that’s the “least worst.”

We make few of these decisions with complete knowledge about how our choice will turn out. We may be missing crucial information, or the decision may rely on elements that are unpredictable — like the weather or others’ behaviour.

When even the most momentary of choices, like what clothes to put on in the morning, can involve juggling a host of considerations (the aforementioned weather, your plans, your mood, what matches what…), the complexity and uncertainty of truly impactful decisions, like choosing a career or how to navigate a difficult personal relationship, can seem monumental.

In the face of so much uncertainty, how do we avoid simply curling up under the bed and never coming out? Here’s the marvel: Even with all the noise, we are nearly always able to make a choice, and often, it works out okay. This is because — likely, without even knowing it — we are applying the concept of expected value to our decisions.

Expected value

Expected value is a method of deciding among options that considers what positive and negative outcomes are possible, and weighs these so that more likely outcomes have a stronger influence on the decision. In simplest mathematical terms, this is “the probability multiplied by the value of each outcome.”

Whether choosing a house or choosing a sandwich, we ask, in short, Am I satisfied that the potential benefits, especially the most likely ones, outweigh the potential downsides, ditto?

In everyday life, we might base our conclusion on vague speculations of what success or failure might look like. However, if you can quantify potential outcomes in some way, you can actually estimate what the best decision might be, using mathematics.

Expected value and turnstile jumpers

Let’s look at an example, albeit not one you should necessarily try at home.

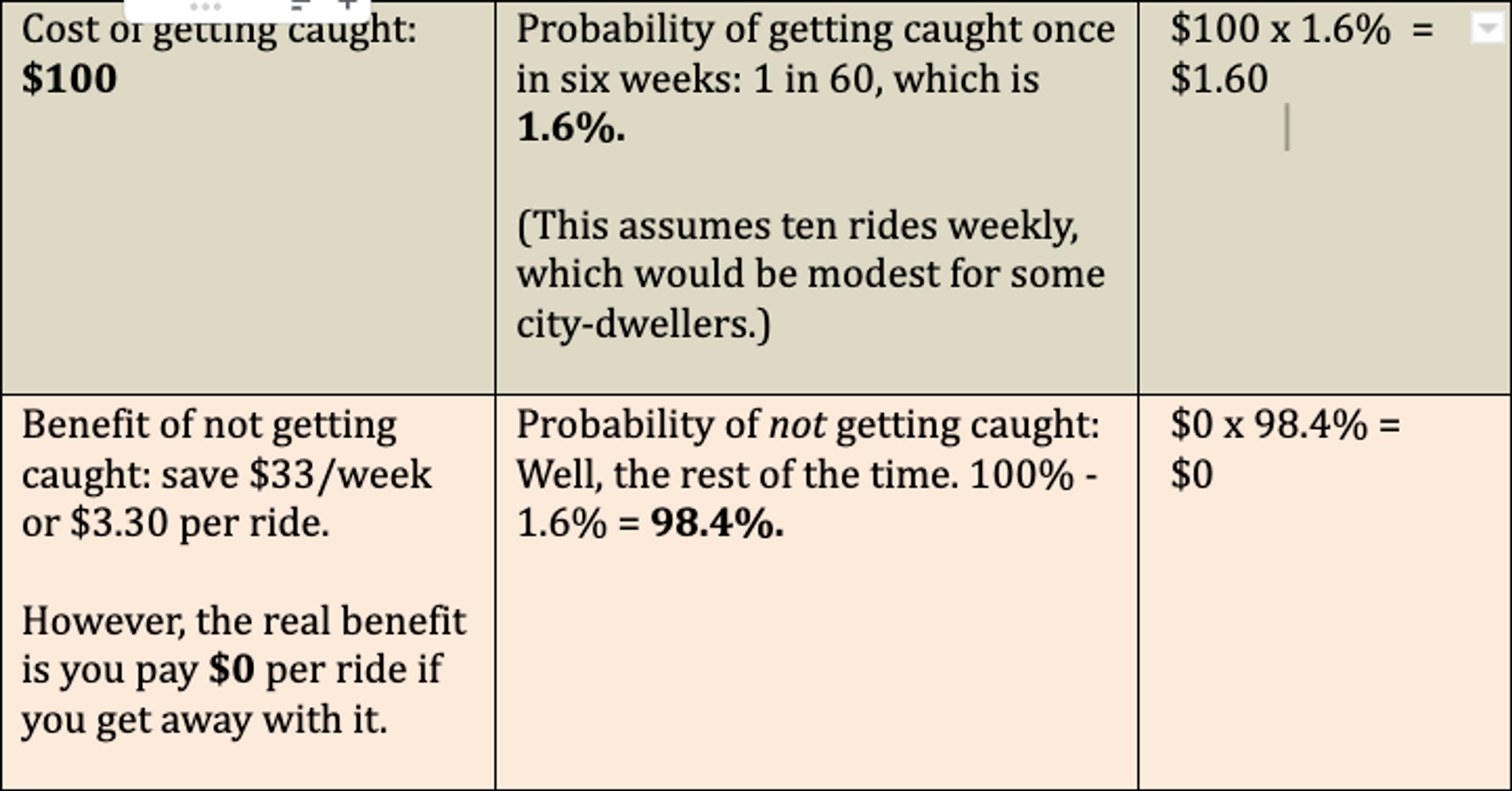
Millions of regular commuters in the New York subway save a lot of money by jumping the turnstile. It’s not that they never get caught; it’s that they know they’ll be caught rarely enough that, in the long run, they’ll save more by paying fines than if they bought tickets. In fact, in 2011 a study showed regular jumpers were only caught about once every 6 to 13 weeks. Let’s do the (rough) math:

The fine for this violation is now (and was then) $100. A current weekly ticket costs $33. So, with minimal math, you might calculate in your head that even with the risk of being caught, a person caught after six weeks would save money since they did not pay for tickets in that time. Since 6 weeks x $33 = $198, they are already ahead of the $100 fine by $98. Even if policing has improved since 2011 and they get caught once every four weeks, they’d still be ahead.

We’ve set aside important moral implications of this act, not to mention harms to the subway’s system’s revenues and resulting effects on commuters. But sticking to mathematics, expected value shows a benefit over time (For a precise breakdown, see "Doing the Math" )

Expected value can make other decisions better

What’s pretty cool is that expected value has much broader implications on your decision-making than just whether or not to do crimes. Statistically speaking, if you make appropriate decisions consistently based on expected value—where you are able to assign numerical values to the severity and likelihood of different outcomes—in the (potentially very) long-run you’re guaranteed to do better than any alternative approach.

That’s why expected value, expressed as a formula, is used in statistics and economics, as well as heavily in pursuits like gambling, investing, planning a lottery, and determining insurance premiums. Experts in these particular sectors have developed methods to assign numerical values, as described, to many or all possible outcomes, and they therefore can use rather simple mathematics to determine what risks will be most likely to turn a profit over time.

Of course, we can't overlook the "expected" part of "expected value." If you calculate the expected value of an action and end up with a positive result, this doesn't mean the action will be beneficial in every case. Gamblers understand well that on any given day, they may win or lose, but over time, actions with positive expected value are expected to see more success than failure. In a repeated course of action—like betting—the more (and more accurately) we apply expected value and choose to do what’s best in expectation, the more likely the results will begin to show the calculated tendency towards positive or negative.

_{Doing the Math}

Expected value and altruism

Expected value allows us to apply a reasonable set of guidelines to somewhat complex decisions and aim for the best outcome. Clearly, then, expected value can be instrumental in making decisions about how best to help others.

If you want to determine (over the long term) how to do the most good with the resources available, or what causes will have the greatest impact, expected value is an important tool. Indeed, such is the project of effective altruism. The Effective Altruism Forum offers this general, simplified example of an expected value calculation around social impact:

Imagine you're choosing between two medical interventions. The first intervention is a drug that succeeds in 60% of cases, and that gives an extra year of healthy life when it succeeds, and has no impact if it fails.

In the case of this drug, there are only two outcomes: success and failure. So the expected value is:

(1 year of life × 60%) + (0 years of life ×40%) = 0.6 expected years of life

Suppose another drug succeeds with a 40% probability, and gives two years of healthy life when it succeeds, but causes harm equal to half a year of healthy life lost when it fails.

Then the expected benefit of this project is:

(2 years of life × 40%)−(0.5 years of life × 60%) = 0.5 expected years of life

Over many cases, the first drug will likely provide more years of healthy life than the second. So if they cost the same, funding the first drug would add more healthy years of life on average.

Uncertainty is the only certainty

Whether it’s distributing malaria nets or curing global blindness, more and more attention is being paid to calculating the expected value of interventions to determine which have the greatest impact in the long term.

Of course, calculating impact is complex, especially since we can’t always rely on precise numerical calculations. Effective-giving groups that make decisions about where to direct resources are the first to acknowledge uncertainty in their calculations and to explain their level of confidence in their conclusions. In certain cases, hard data may not yet have been scientifically generated, and some interventions simply aren’t easy to quantify numerically. Just consider the difficulty of calculating the impact of wearing masks during the COVID-19 pandemic; it’s very difficult to say with any certainty how many lives were saved. Or consider how to measure the effects of a long-term political effort: There are so many players and external factors that quantifying the effect of your particular work on the issue is impossible.

This uncertainty, however, is precisely what makes the concept of expected value so important. In the absence of hard numbers, we can still use this tool to favor choices that tend towards success, over time.

To allow expected value to be gauged even in situations of uncertainty, effective altruists have developed heuristics — thinking strategies — that break down the idea of expectation into distinct categories. The most well known of these is the framework represented by impact, neglectedness, and tractability (discussed in detail here).

Such strategies still make use of available evidence, but also bridge gaps in the data by applying careful reasoning, supported by cause-and-effect evidence, about possible courses of action. In this way, expected value helps us avoid situations where we might rely on pure chance or be swayed by moving appeals (sad-eyed puppies?), alarming images, or personal predispositions. This guides us towards interventions that are objectively more effective than others.

Expected value also reveals “hidden” value

There are other, more subtle benefits of using expected value in giving decisions. First, it allows us to look with objective eyes at interventions that seem to have a small chance of success. The organisation 80,000 Hours has pointed out that donors tend to neglect riskier or more innovative options that can’t yet point to a track record, even if they have great potential.

This is the basis for an approach in altruism called hits-based giving. If the potential impact of a charity’s approach is high enough, it might be that it’s worth funding even if its chances for success are slim — merely because the potential positive outcome is so enormous. An oft-cited example: Norman Rockefeller invested in Norman Borlaug’s somewhat unlikely research into agricultural productivity, and Borlaug's work led to the development of high-yielding wheat strains that have brought millions of people out of hunger.

Investing — thoughtfully — in possibly risky but promising interventions can, over time, lead to a few huge breakthroughs — programs which expected value revealed ahead of time to have strong potential. A simplified case in point: a $1 million grant with a 99% chance of having no effect and a 1% chance of preventing 50,000 premature deaths, has the same base expected value as a $1 million grant with a 100% chance of preventing 500 premature deaths. Despite the higher risk, if one follows expected value, the former example arguably is as worthy to fund as the latter.

Likewise, in forcing a long-term perspective, expected value can lead us to look further into the future and acknowledge the value “hidden” there — potential benefits over the horizon that may need to be recognized when setting priorities.

Finally, even if a particular calculation of expected value leads to a less-than-desired outcome, the process of using it regularly as we struggle with decisions around giving or otherwise forces a rigour and reflection that itself can make our decision-making more effective. The deliberative nature of the process may allow us to see factors we would otherwise miss.

Bending the curve

All this is why expected value is so crucial in decisions about giving, just as in the most important real-life choices. The stakes are high as we decide where our effort or dollars can alleviate the most suffering or save the most lives. Taking the time to use the available tools to look for the most promising expected value might mean the difference between saving an additional life, and not.

Of course, in life we can’t be expected, nor do we have the time, to apply expected value to every decision. We must rely on mental shortcuts, estimates, and even gut feelings to get through our decision-filled days.

But where it matters, in the aggregate and over the long term, expected value builds a rough framework of rationality over our otherwise slapdash decisions. While nothing is certain, if we follow expected value in our lives and in our giving decisions, we will win more than we lose, we will shuffle — even if sometimes haltingly — towards happiness, and we will bend the curve towards the world we want to see.